LTI
| Hlavní stránka | Laboratorní modely | Vyučované předměty | Vybavení | Historie | Správce laboratoře | Pro studenty | Odkazy | |
Popis systémů a jejich analýzaV teto kapitole se budeme zabývat LTI systémy. Pro předměty SAM a SRI je třeba analyzovat a řídit pouze SISO systémy. Práce s MIMO systémy je obdobná, jen je místo přenosu třeba používat matice přenosu. Funkce pro vytvořeni přenosuZákladním popisem již linearizovaného systému je jeho přenos. Abychom jej mohli zadat Matlabu máme připraveny některé funkce. Ty vytvoří přenos obsahující symbolickou proměnnou s. tf([c],[j]) - Vytvoří přenos z vektoru c a j, kde prvky vektoru c jsou koeficienty polynomu čitatele a prvky vektoru j jsou koeficienty polynomu jmenovatele. >> F = tf([4],[1 8 15])
zpk([z],[p],k) Vytvoří přenos z vektoru z a p, kde prvky vektoru z jsou nuly systému (kořeny čitatele) a prvky vektoru p jsou póly systému (kořeny jmenovatele). Parametr K udává stejnosměrné zesíleni. Jak je vidět z následujícího příkladu, pokud systém neobsahuje žádné nuly může být vektor z i prázdný. >> F = zpk([],[3 5], 4)
V případě že chceme přenos nějak upravovat (přidat astatismus nebo jiný pól či nulu), nemusíme jej pomocí těchto funkcí vždy tvořit znova. Pouhé vynásobení výrazem 1/(s+3) však pól do přenosu nepřidá. Nepomůže ani definice s jako symbolické proměnné pomocí syms s. Proměnná s totiž není definována jako přenos, a proto je nahlášena chyba násobení. Abychom mohli s proměnnou s pracovat jako s přenosem musíme nejdříve použít například příkaz s = tf([1 0],[1]). Poté již vše funguje korektně.
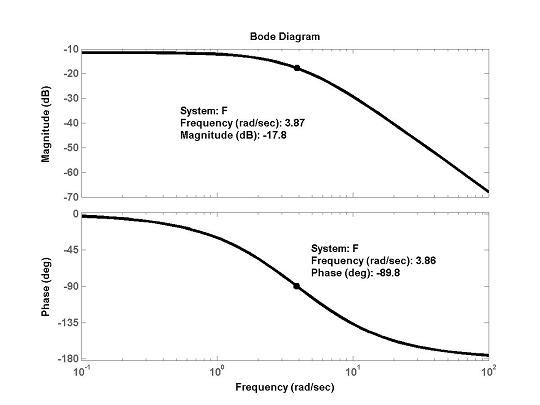
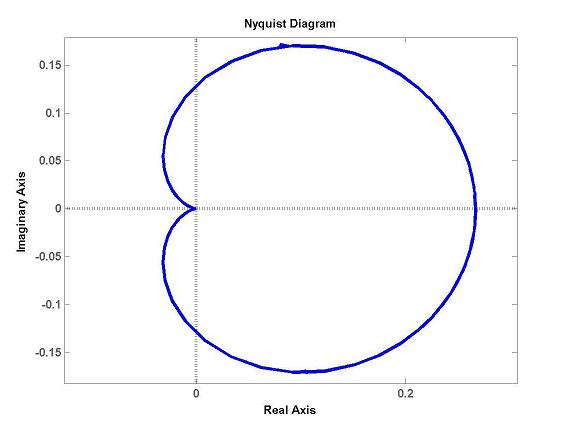
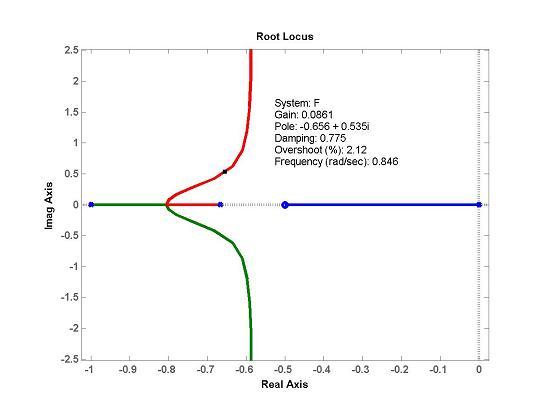
S takto vytvořenými přenosy lze provádět algebraické operace jako násobení (sériové řazení systémů), sčítat (paralelní řazení systémů), dělení (1/(G+1) - zpětná vazba) a podobně. Analýza ve frekvenční oblastiK této analýze je připraveno několik funkcí zobrazující frekvenční charakteristiky soustavy. Jelikož některé vlastnosti těchto funkcí nejsou zcela optimální, byly vytvořeny jejich analogie lépe vyhovující výuce. Zde je uveden pouze popis funkcí integrovaných do prostředí Matlab. Všem funkcím je nutno zadávat jako systémy proměnné typu přenos. Tedy volání funkce bode() s způsobem bode(1/(s+3)) možné není. Je nutno použít buď již vytvořený přenos nebo trik s definicí s jako přenosu. bode(SYS, {w_min, w_max}) - Zobrazí amplitudovou a fázovou charakteristiku v logaritmických souřadnicích. Systémů je možno zadat i více. Nepovinné parametry w_min a w_max určují pevně počáteční a koncovou frekvenci zobrazení. Pokud příkaz zadáme způsobem >>[Amplituda, Faze] = bode(...) nebude zobrazen graf, ale hodnoty amplitudy a fáze budou zapsány do polí Amplituda a Faze. Myší můžeme na průběhu charakteristiky pohybovat kurzorem a odečítat hodnoty amplitudy a fáze. Příklad výstupu (používáme přenos F vytvořený v příkladu funkcí tf nebo zpk): nichols(SYS, {w_min, w_max}) - Zobrazí nicholsovu charakteristiku soustavy. Další možnosti a vlastnost stejné jako u funkce bode(). nyquist(SYS, {w_min, w_max}) - Zobrazí nyquistovu charakteristiku soustavy. Další možnosti a vlastnost stejné jako u funkce bode(), jen vektory do kterých jsou zapisovány hodnoty mají význam [Re, Im]. Výstup funkce nyquist(F) (proveden zoom): margin(sys) - Vypočte fázovou a amplitudovou bezpečnost soustavy a jim odpovídající kritické frekvence. Analýza polohy pólů a nulZákladním nástrojem je funkce rlocus(), která zobrazí polohu pólů a nul otevřené smyčky a trajektorie jejich pohybu v závislosti na zesílení (GMK). Opět můžeme kurzorem průběh sledovat a odečítat parametry při daném zesílení.
Druhým, již poměrně komplexním nástrojem, který může sám dobře posloužit k samotnému návrhu regulátoru je rltool. Do něj lze importovat přenos řízeného systému, prohlédnout GMK a přidáváním pólu a nul regulátoru, jejich přemísťováním, případně změnou zesílení zjistit parametry regulátoru, který má požadované vlastnosti. Analýza v časové oblastiK simulacím chování systémů v časové oblasti používáme funkce impulse() a step(). Jejich výstupem je časová odezva na diracův impuls resp. jednotkový skok. Syntaxe je u obou funkcí stejná step(SYS,< t>) nebo impulse(SYS,< t>), kde SYS je přenos systému a t je doba simulace. Zadáme-li na místo skaláru t vektor, je simulace vypočtena v časech zadaných prvky vektoru. Nezadáme-li t vůbec, bude zvoleno automaticky. Stejně jako u funkce bode() lze zadat funkci systémů více, a také výsledek funkce přiřadit struktuře [Y T]. Toto je výhodné například porovnáváme-li naměřenou odezvu reálného systému s odezvou linearizovaného systému zadaného přenosem. Oba získané vektory pak snadno vykreslíme funkcí plot(). Funkce určené k propojování systémůTyto funkce mají větší význam až při práci s MIMO systémy. U SISO systémů stačí aritmetické operace s přenosy jednotlivých větví. Jejich podrobnější popis nalezne čtenář v dokumentaci Matlabu, zde je uveden pouze stručný popis využití. series(sys1,sys2,[OUT1],[INP2]) - Propojí dva systémy kaskádně. Vektory OUT1 a IN2 udávají který výstup je spojen se kterým vstupem. parallel(sys1,sys2,[OUT1],[OUT2],[INP1],[INP2]) - Propojí dva systémy paralelně. Vektory opět udávají propojení. feedback(sys1,sys2,[OUT],[INP]) - Zapojí jeden systém do zpětné vazby druhého.
|