Kulička na tyči K1
| Hlavní stránka | Laboratorní modely | Vyučované předměty | Vybavení | Historie | Správce laboratoře | Pro studenty | Odkazy | |
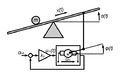
Model Kulička na tyči K1 simuluje problémy objevující se při řízení nestabilních systému jako např. v letectví, při startu raketoplánu, řízení exotermní reakce v chemickém průmyslu, řízení vertikální polohy plazmatu v tokamaku apod. Ve výuce můžeme model využít např. k aplikaci základního řízení (PID regulace) náklonu tyče α pomocí vstupu αref nebo polohy kuličky x(t) pomocí vstupu αref. Dále je možné použít Kalmanův filtr k odhadování náklonu tyče α(t) na základě měření vstupu αref a polohy kuličky x(t) či navrhnout pokročilé metody řízení jako je LQ regulátor nebo explicitní MPC regulátor. Laboratorní model je zobrazen na obr. 1.
Schéma a konstrukce modelu
Model kuličky K1 je složen z elektromotoru, tyče a ocelové kuličky, která se volně pohybuje v kolejnicích umístěných na tyči. Elektromotor je řízen ve zpětné vazpě P (proporcionálním) regulátorem a umožňuje naklánět tyč přibližně v rozsahu +/ - 10° od vodorovné polohy. Vstupem modelu je pak žádaný úhel náklonu tyče αref. Skutečný úhel náklonu tyče α je snímán servopotenciometrem připevněným na zadní část osy tyče. Kulička se pohybuje po tyči, respektive po dvou rovnoběžných drátech, pomocí kterých je také snímána její poloha x(t). Jeden z drátů je připojen na zdroj napětí a kulička mezi dráty funguje jako jezdec potenciometru, který převádí část napětí na druhý drát. Všechny veličiny jsou převedeny na elektrická napětí. Součástí modelu je přístrojová skříň obsahující zdroj (obr. 2). Model se zapíná páčkovým vypínačem, který se nachází na zadní stěně tohoto zdroje a zapnutí je indikováno zelenou LED diodou na tomto zdroji. Kapacitu u filtru pro snímání polohy kuličky je vhodné nastavit na hodnotu 1M. Přepínač pro ovládání náklonu tyče je pro komunikaci s Matlabem třeba nastavit do polohy EXT. Nastavením přepínače do polohy MAN je náklon tyče možné ovládat ručně levým potenciometrem.
Informace pro studenty
Obecné informace
Z matematického hlediska model představuje nelineární astatický systém. Model servomechanismu je možné řídit pomocí PC s programem Matlab/ Simulink a Real Time Toolboxu, kde jsou všechny veličiny převedeny na bezrozměrná čísla obvykle v intervalu (-1, +1). Náklon tyče je také možné řídit ručně (levým potenciometrem na zdroji).
Pokyny pro práci s modelem
- Výchozí náklon tyče volte nulový, výchozí polohu kuličky od 10 cm od středu tyče na levo až do kraje!
- Hodnotu požadovaného náklonu tyče po skončení měření po případné změně vraťte na nulovou hodnotu!
Důležité vztahy
Schématicky zobrazený model je na obr. 3.
Význam použitých symbolů je následující:
αref [°] je žádaný náklon tyče, α(t) [rad] je skutečný úhel náklonu tyče, x(t) [m] je poloha kuličky, kp [-] je zesílení P regulátoru, um(t) [V] je napětí motoru, φ(t) [rad] je úhel natočení hřídele motoru, m [kg] je hmotnost kuličky.
Pro matematický popis modelu využijeme rovnice popisující činnost stejnosměrného motoru:
<math>L\frac{\mathrm{d} i(t)}{\mathrm{d}t}=-R\,i(t)-k_e\,\omega(t)+u(t)</math>, (1)
<math>J\frac{\mathrm{d} \omega(t)}{\mathrm{d}t}=k_m\,i(t)-b\omega(t)-M_z\,(t)</math>, (2)
<math>\frac{\mathrm{d} \varphi(t)}{\mathrm{d}t}=\omega(t)</math>, (3)
kde i(t) [A] je proud motoru, ω(t) [rad s-1] je otáčky motoru, u(t) [V] je vstupní napětí motoru, Mz [N m] je vnější zatěžovací moment, R [Ω] je elektrický odpor motoru, L [H] je indukčnost motoru, J [kg m2 s-1] je moment setrvačnosti motoru, ke [s V-1] je elektrická konstanta motoru, km [kg m2 s-2] je mechanická konstanta motoru, b [kg m2 s-1] je konstanta tření motoru.
Pří odvození rovnic popisující chování kuličky vychazíme ze vztahu pro zachování mechanické energie, zároveň uvažujeme vliv tření kuličky o dráty. Rovnice jsou potom
<math>\frac{\mathrm{d} v(t)}{\mathrm{d}t}=\frac{g}{1+\frac{2}{5}\,(\frac{R_k}{r})^2}\sin(\alpha(\varphi())-\,\delta v(t))</math>, (4)
<math>\frac{\mathrm{d} x(t)}{\mathrm{d}t}=v(t)</math>, (5)
kde v(t) [m s-1] je rychlost pohybu kuličky, g [m s-2] je gravitační zrychlení, Rk [m] je poloměr kuličky, r [m] je poloměr odvalování kuličky mezi dráty, δ [-] je koeficient tření.
Volba vstupních a výstupních veličin systému
Jako vstupní veličinu volíme αref, výstupní veličiny jsou potom α(t) a x(t).
Soubory
- Média:K1-id.pdf - zadání pro identifikaci laboratorního modelu
- Média:K1-reg.pdf - zadání pro řízení laboratorního modelu
Literatura
1. FUKA, Jindřich; JOHN, Jan; KUTIL, Michal. Učebnice SARI [online]. Dostupné z WWW: <http://dce.felk.cvut.cz/sari>
2. HOLEČEK, Jan. Laboratoř teorie automatického řízení K26 [online]. Dostupné z WWW: <http://support.dce.felk.cvut.cz/lab26>
3. HALÍŘ, Lukáš. K1 – Kulička na tyči UTIA. 2010