Inverzní kyvadlo P1
| Hlavní stránka | Laboratorní modely | Vyučované předměty | Vybavení | Historie | Správce laboratoře | Pro studenty | Odkazy | |
Laboratorní model Inverzní kyvadlo P1 byl sestaven a uveden do provozu Tomášem Hanišem v roce 2003. Základem tohoto modelu byl tehdy model firmy Quanser. Současná podoba modelu vznikla dalšími úpravami v rámci bakalářské práce Lukáše Kratochvíla [1] v roce 2008. Model simuluje řadu procesů vyskytujících se v reálném světě, např. simuluje chování rakeplánu při startu. Model je možné v rámci výuky využít k řízení polohy kyvadla a jeho stabilizaci (např. pomocí PID regulátorů, LQR řízení). Fotografie modelu je na obr. 1.
Schéma a konstrukce modelu
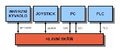
Celý model Inverzní kyvadlo P1 je složen ze 4 samostatných částí zapojených do hlavní skříně. Situace je zobrazena na obr. 2 a je tedy zřejmé, že části jsou: vlastní model inverzního kyvadla, joystick, PC, PLC a již zmíněná hlavní skříň. Jednotlivé části si nyní popíšeme.
Hlavní skříň
Hlavní skříň obsahuje obvod pro přepínání řízení mezi PC a programovatelným automatem, současně slouží jako hlavní napájecí zdroj. Do hlavní skříně jsou zapojeny zbylé části modelu. Detail hlavní skříně je zobrazen na obr. 3. Z obrázku je patrný panel s konektory PLC, X1K, X2K, joystick a pendulum, původní rozhraní umístěné nad tímto panelem se již nepoužívá. Na zadní stěně skříně je vypínač, kterým se celý laboratorní model zapíná.
Inverzní kyvadlo
Vlastní model inverzního kyvadla je složen z vozíku poháněného stejnosměrným motorem přes ozubené kolo po ozubici. Na vozíku je zavěšeno kyvadlo, které je volně otočné na hřídeli. Snímání polohy vozíku a snímání náklonu kyvadla je zajištěno dvěmi IRC snímači. Model dále obsahuje 4 spínače: 2 horní (KLN a KPN) slouží k hardwarovému odpojení motoru od napájení, 2 dolní (KLD a KPD) jsou využity pro účely řízení. Detail inverzního kyvadla a popis důležitých částí je zobrazen na obr. 4 a v tab. 1.
| označení v obrázku | část |
|---|---|
| 1 | připojovací sběrnice |
| 2 | koncový spínač KLD |
| 3 | koncový spínač KLN |
| 4 | vozík |
| 5 | koncový spínač KPN |
| 6 | koncový spínač KPD |
| 7 | ozubice |
| 8 | snímání polohy vozíku přes IRC |
| 9 | kyvadlo |
| 10 | pohon vozíku stejnosměrným motorem |
| 11 | snímání náklonu kyvadla přes IRC |
| 12 | joystick |
PC
Připojení modelu k PC je realizováno pomocí převodníkové karty Humusoft MF624 a Real Time Toolboxu pro Matlab, který umožňuje řízení modelu v reálném čase.
PLC
Model je připojen k programovatelnému automatu (PLC) řady ControlLogix 1756 (firma Rockwell Automation). K automatu je naistalován PC software umožňující jeho programování, zároveň však plní řadu dalších užitečných funkcí jako např. monitorování chodu systému apod.
Joystick
Původním záměrem joysticku bylo využití k manuálnímu řízení modelu. To se však v praxi ukázalo jako nereálné, proto se od tohoto způsobu řízení upustilo. Přesto má využití joysticku praktický význam – je možné použít ho jako zdroj referenční polohy vozíku. Detail joysticku je na obr. 5.
Informace pro studenty
Obecné informace
Z matematického hlediska model představuje nelineární astatický systém. Jak již bylo zmíněno výše, model můžeme řídit dvěma způsoby – buď pomocí PC s programem Matlab/ Simulink a Real Time Toolboxu, kde jsou všechny veličiny převedeny na bezrozměrná čísla obvykle v intervalu (-1, +1), nebo pomocí PLC.
Pokyny pro práci s modelem
- Při spuštění nemějte ruce ani žádné předměty v dráze vozíku!
- Pro vyšší hodnoty vstupního napětí zkraťte dobu simulace, aby nedocházelo k poškozování kyvadla!
Důležité vztahy
Při odvozování stavového popisu systému vycházíme z následujících rovnic:
<math>I\,\frac{\mathrm{d^2} \theta (t)}{\mathrm{d}t^2}+k\,\frac{\mathrm{d} \theta (t)}{\mathrm{d}t}+m_p\,g\,l\,\sin\theta(t)=-m_p\,l\,\frac{\mathrm{d^2} x(t)}{\mathrm{d}t^2}\cos\theta (t)</math>, (1)
<math>(m_t + m_p)\frac{\mathrm{d^2} x (t)}{\mathrm{d}t^2}+b\frac{\mathrm{d} x (t)}{\mathrm{d}t}+m_p\,l\,\frac{\mathrm{d^2} \theta (t)}{\mathrm{d}t^2}\cos\theta(t)- m_p\,l\,\frac{\mathrm{d} \theta^2 (t)}{\mathrm{d}t}\sin\theta(t)=c\,u(t)</math>, (2)
kde θ(t) [rad] je náklon kyvadla, x(t) [m] je poloha vozíku, u(t) [V] je napětí na motoru vozíku, I [kg m2] je moment setrvačnosti kyvadla vztažený k ose rotace, mc [kg] je hmotnost vozíku, mp [kg] je hmotnost kyvadla, g [m s-2] je gravitační zrychlení, l [m] je vzdálenost těžiště od středu rotace kyvadla, k [kg m2 s-1] je koeficient viskózního tření kyvadla v ose rotace, b [kg s-1] je koeficient viskózního tření ozubeného kola vozíku s ozubnicí, c [N] je převodní konstanta převádějící vstup na sílu vyvinutou motorem.
Pozn.: Hmotnost vozíku s kyvadlem je 1170 g, hmotnost kyvadla se šrouby je 157 g.
Volba vstupních a výstupních veličin systému
Jako vstupní veličinu volíme napětí na motoru u(t), výstupní veličiny potom představují náklon kyvadla θ(t) a poloha vozíku x(t).
Soubory
- Média:P1-id.pdf - zadání pro identifikaci laboratorního modelu
- Média:P1-reg.pdf - zadání pro řízení laboratorního modelu
Literatura
- ↑ KRATOCHVÍL, Lukáš. Inverzní kyvadlo, 2008